正負の数をわかりやすく解説！その意味や計算時の注意点をチェック

こんにちは！家庭教師のファミリーです。

 

小学校の算数では、正の数で足し算や引き算、掛け算や割り算などの計算を学びました。

 

中学校の数学では、正の数に加えて負の数についても学び、正と負、両方の数を使った計算を学びます。

 

この正負（せいふ）の数については、特に小学校で習っていない負の数に苦手意識を持つ人が多いです。

 

でも、イメージをしっかりつかみ、ルールを把握すれば、正負の数の計算は決して難しくありません。

 

そこで今回は、正負の数とその計算についてわかりやすく解説します。

 

頭の中に数直線を思い浮かべながら、ポイントを確認していきましょう！

 

 

 

 

正負の数をわかりやすく解説！

まずは、正負の数がどのようなものなのか説明していきましょう。

 

 

 

正負の数とは

正負の数とは、「正の数」と「負の数」のこと。

それぞれ次のような数字を指します。

 

 

• ・正の数･･･0より大きい数字（+プラス）

• ・負の数･･･0より小さい数字（-マイナス）

 

※0は正の数にも負の数にもならない

 

0より大きい数字である正の数には、数字の前に「+」がつきます。

 

また、0より小さい数字である負の数には、数字の前に必ず「-」がつきます。

 

これらの符号は、「足す」「引く」と読むのではなく、英語でそれぞれ「プラス」「マイナス」と読みます。

 

 

 

正負の数を理解するには数直線がカギ

まずは、頭の中に数直線を思い浮かべてみてください。

 

絶対値の勉強で既に習ったかと思いますが、数直線とは、直線の上に目盛りを書いて数を表したものです。

 

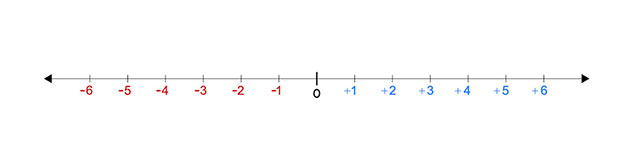
数直線で考える場合、絶対値を理解しておく必要があります。

絶対値とは、原点である0からの距離を表す値のことです。

 

たとえば-3と+3の絶対値は、原点である0からの距離が同じなのでどちらも3です。

 

これが頭に入っていると、以下の2点のルールがわかります。

 

• ・正の数は絶対値が大きいほど大きくなる
• ・負の数は絶対値が大きいほど小さくなる

 

この2点のルールについて、詳しく見ていきましょう。

 

数直線で見ると、0を真ん中にして右側が正の数（プラス）、左側が負の数（マイナス）になります。

そして、プラスの数字とマイナスの数字は、0を真ん中にして左右対称にふられます。

また、数は右にいくほど大きく、左にいくほど小さくなります。

 

例えば、「+6、-6、+2、-2 」という4つの数字があったとします。

 

数直線で見ると、4つの数字のうち一番左側にくる数字は-6。

その右側に-2がきます。

0を挟んでさらに右側に+2がきて、一番右側には+6がきます。

 

先ほど述べたように、数直線では右にいくほど数が大きく、左にいくほど小さくなるため、この4つの数字を小さい順に並べると、「-6、-2、+2、+6」となります。

 

負の数では、正の数と違って、符号「-」の後ろの数字が大きいほど、数の大きさは小さくなるので注意しましょう。

 

正負の数の基本をまとめると以下の3つになります。
数直線をイメージしつつ覚えておいてくださいね。

 

 

• ・0よりも大きな数（数直線の0より右側）が正の数である

• ・0よりも小さな数（数直線の0より左側）が負の数である

• ・数直線の右にいくほど数は大きく、左にいくほど数が小さい

 

 

 

 

正負の数を理解するポイントは？

基本を学習したところで、正負の数をさらに深く理解するためのポイントを見ていきましょう。

 

 

 

プラスの符号は省略可、マイナスの符号は省略不可

小学校の算数では、正の数だけで計算を行ってきました。

でもこのとき、数字の前に「+（プラス）」の符号なんてつけていませんでしたよね。

 

実は、正の数の前につく「+（プラス）」の符号は、省略することができます。

正の数にわざわざ「+（プラス）の符号をつけることは、あまりありません。

小学校の算数で扱っていた数字も、私たちが日々の買い物で見る物の値段も、ゲームのレベルも、全てプラスの符号を省略した正の数なのですね。

 

ただし、気をつけておきたいのが、負の数の前につく「-（マイナス）」の符号は省略できないということ。

「-（マイナス）」の符号を省略してしまうと、負の数かどうかの判断がつきません。

そのため、負の数には必ず「-（マイナス）」の符号がつけられます。

 

ここで覚えておきたいのは、以下の3点。

 

 

• 正の数の「+（プラス）」の符号は省略可能

• 負の数の「-（マイナス）」の符号は省略不可

• 符号がない場合は正の数

 

 

これは正負の数のルールです。

 

 

 

符号と数字はセットで考える

もうひとつ、ポイントとして押さえておきたいのは、符号と数字はセットで考えるということ。

数字とその数字の前についている符号は切り離さず、セットで考えるようにしてください。

 

この考え方をしないと、次のようなミスが起こります。

 

誤）-4+2=-6

-4-2=-2

 

上の式では、まず4+2をして、その後に「-（マイナス）」の符号をつけてしまっています。

下の式でも同じで、4-2をした結果の数に「-（マイナス）」の符号をつけてしまったのでしょう。

 

どちらも、-4についている「-（マイナス）」の符号を、最初に4から離して計算してしまっているのですね。

 

これらの計算は間違いです。

 

正しく計算するためには、符号と数字はセットで考え、勝手に符号を切り離して計算してはいけません。

 

正しい答えは、以下のとおりです。

 

正）-4+2=-2

-4-2=-6

 

わかりやすく、下の数直線でも考えてみましょう。

 

-4は0から左方向に4目盛り進んだ状態です。

+2は、右方向に2目盛り進むということなので、−4から右方向に2目盛り進みます。

すると、答えは-2となります。

 

下の式では、0から左に4目盛り進んだ状態である-4から、-2なので、さらに2目盛り左方向に進んだ状態になります。

よって、答えは-6となります。

 

これらの式の場合、「-4を右に2ずらす」「-4を左に2ずらす」というように考えるとわかりやすいですね。

 

計算時に勝手に符号を取ったりつけたりしないよう、気をつけましょう。

 

 

 

 

正負の数を使う計算での注意点もチェック

次に、正負の数を使った計算問題での注意点について説明していきます。

 

 

 

正負の数と足し算・引き算（加法・減法）

数直線をしっかり思い浮かべることができれば、正負の数の足し算・引き算はしやすくなります。

 

でも、数字が大きくなるとそれも難しくなりますよね。

 

そこで正負の数の足し算・引き算のルールとして、次の3点を押さえておいてください。

 

 

1. 同じ符号の2つの数を足し算・引き算するときには、それぞれの数の絶対値の和に共通の符号をつける
2. 異なる符号の2つの数を足し算・引き算するときには、それぞれの数の絶対値の差に、絶対値が大きい方の数字の符号をつける
3. 負（マイナス）の数を引くと、正（プラス）の数になる

 

 

具体例を挙げて見てみましょう。

 

 

①の例）同じ符号の2つの数を足し算・引き算するときには、それぞれの数の絶対値の和に共通の符号をつける

-8+（-3）=-11

→絶対値を足して11。共通の符号である-をつけて答えは「-11」。

 

 

②の例）異なる符号の2つの数を足し算・引き算するときには、それぞれの数の絶対値の差に、絶対値が大きい方の数字の符号をつける

（-5）+6=1

→絶対値の差が1。絶対値が大きい方の符号+をつけて+1。+の符号は省略できるので答えは「1」。

 

③の例）負（マイナス）の数を引くと、正（プラス）の数になる

7-（-5）=12

→負の数を引くと、正の数になるので、この場合は7+5となり、答えは「12」。

 

 

このルールを知っておけば、数直線を思い浮かべる方法を取らなくても、正負の数の足し算・引き算が素早くできるようになります。

 

 

 

正負の数と掛け算・割り算（乗法・除法）

次に学習するのは、正負の数の掛け算・割り算についてです。

 

正負の数の掛け算・割り算では、次の4種のルールを押さえておきましょう。

 

 

• 正の数×（÷）正の数＝正の数（答えは+）

• 負の数×（÷）負の数＝正の数（答えは+）

• 正の数×（÷）負の数＝負の数（答えは-）

• 負の数×（÷）正の数＝負の数（答えは-）

 

 

つまり、「同じ符号同士の掛け算・割り算の答えは正の数」「異なる符号同士の掛け算・割り算の答えは負の数」になります。

 

上記4つのルールを実際の問題にあてはめると、次のようになります。

 

【掛け算の例】

① 2×3=6

② -2×（-3）=6

③ 2×（-3）=-6

④ -2×3=-6

 

 

【割り算の例】

① 4÷2=2

② -4÷（-2）=2

③ 4÷（-2）=-2

④ -4÷2=-2

 

 

割り算や掛け算はそのまま数字を見て行い、符号は先ほどのルールに従って選択すれば、正しい答えを出すことができます。

 

 

 

 

正負の数は数直線とルールを押さえるとわかりやすくなる！

正負の数は0を基準として、正の数と負の数で成り立っています。

 

正の数は0より大きい数字のことで、符号として数字の前に+がつき、負の数は0より小さい数字のことで、符号として数字の前に-がつきます。

 

ただし、正の数の+の符号は省略できます。

符号のついていない数字は正の数だと考えてください。

 

正負の数の計算では、絶対値をもとにした基本のルールがあります。

 

これらのルールを使えば計算はスムーズに行えるので、必ず覚えておくようにしましょう。

 

今はまだ素早く計算できない人も、計算を重ねるうちに直感的にルールを適用できるようになるので安心してください！

 

家庭教師のファミリーでは、生徒ひとりひとりに合ったマンツーマンでの学習を提供しています。

将来的にも役立つ自立学習力を身につけることが可能です。

 

詳しい情報については、資料請求や無料体験、お電話などでお話ししておりますので、お気軽にお問い合わせください！